En este post vamos a resolver los reactivos del 31 al 40, de la cuarta parte de los ejercicios de Pensamiento Matemático del simulacro de ingreso a UABC.

Ir a los reactivos del 21 al 30 del simulacro examen UABC
Resuélvelos por tu cuenta antes de mirar la solución. La finalidad del simulacro es acercarte a la prueba real. La única forma de lograr una buena calificación es a través de la práctica constante.
Al consultar las respuestas, analiza los procedimientos e intenta pensar en caminos alternativos que acorten el tiempo.
Reactivo 31
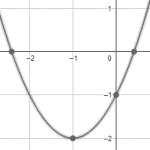
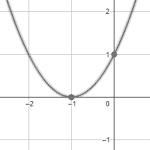
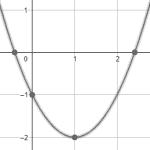
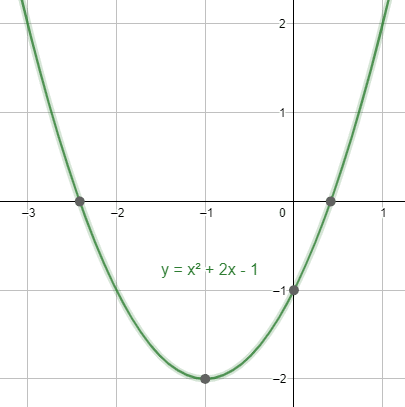
A partir de la parábola y={x}^{2}+2x-1 , indique cuál de las siguientes imágenes corresponde con su gráfica.
Solución:
Este problema lo podemos resolver de dos formas: aplicando completación de cuadrados o mediante igualación de términos al desarrollar la ecuación ordinaria de la parábola. Ambas alternativas son equivalentes en complejidad, por tanto, nos tomamos la libertad de emplear completación de cuadrados.
La completación de cuadrados consta en llevar una expresión cuadrática a otra en forma de binomio cuadrado.
y={x}^{2}+2x-1\to y={\left(x+a\right)}^{2}+b
Comenzamos separando el término lineal en 2ax .
y={x}^{2}+2\left(1\right)x-1
En este caso, el término a=1 . Por tanto, al desarrollar el cuadrado debería quedar un +1. Como está un -1, debemos sumar y restar 1.
y={x}^{2}+2\left(1\right)x-1+1-1\to y={x}^{2}+2\left(1\right)x+1-2
Ahora, aplicamos el producto notable del binomio cuadrado en sentido contrario.
y={x}^{2}+2\left(1\right)x+1-2\to y={\left(x+1\right)}^{2}-2
Si pasamos el 2 a sumar al otro lado, tenemos las coordenadas del vértice.
y+2={\left(x+1\right)}^{2}\to v\left(-1, -2\right)
Comparando con las gráficas de los incisos, concluimos que la respuesta correcta es la a).
Consulta las fechas de la siguiente convocatoria a la UABC
Reactivo 32
Una recta pasa por el punto P\left(-1, 1\right) y es perpendicular a otra cuya ecuación es y=-2x . Calcule la ecuación de la recta que pasa por el punto P .
- y=\frac{1}{2}x+\frac{3}{2}
- y=\frac{1}{2}x+\frac{1}{2}
- y=\frac{1}{2}x-\frac{3}{2}
Solución:
Para encontrar la ecuación de la recta solicitada, necesitamos la pendiente y un punto. El punto lo indica el enunciado. La pendiente la extraemos de la otra recta, con la condición de perpendicularidad:
{m}_{2}=-\frac{1}{{m}_{1}}
Sustituimos la primera pendiente en la fórmula:
{m}_{2}=-\frac{1}{-2}=\frac{1}{2}
Sustituimos en la ecuación el punto pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)\to y-1=\frac{1}{2}\left(x+1\right)
Despejando y reacomodando:
y=\frac{1}{2}x+\frac{1}{2}+1\to y=\frac{1}{2}x+\frac{3}{2}
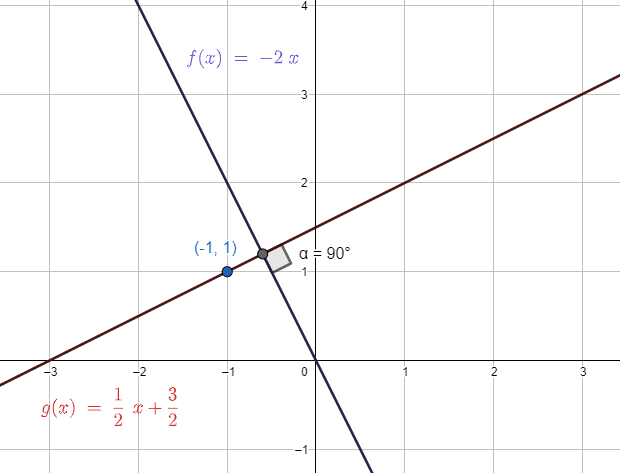
Concluimos que la respuesta correcta es el inciso a).
Todo sobre la nueva guía para el examen de ingreso a UABC
Reactivo 33
¿Cuál es la ecuación de la elipse con vértice en el punto \left(1, 1\right) y que pasa por los puntos A\left(1, 4\right) y B\left(0, 1\right) ?
- \frac{{\left(x-1\right)}^{2}}{9}+\frac{{\left(y-1\right)}^{2}}{1}=1
- \frac{{\left(x-1\right)}^{2}}{1}+\frac{{\left(y-1\right)}^{2}}{9}=1
- \frac{{\left(x+1\right)}^{2}}{1}+\frac{{\left(y+1\right)}^{2}}{9}=1
Solución:
Comencemos escribiendo la ecuación ordinaria de la elipse.
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}+\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Comenzamos sustituyendo el centro en la ecuación.
\frac{{\left(x-1\right)}^{2}}{{a}^{2}}+\frac{{\left(y-1\right)}^{2}}{{b}^{2}}=1
Ahora, sustituimos los dos puntos dados para establecer un sistema de ecuaciones.
ec1: \frac{{\left(1-1\right)}^{2}}{{a}^{2}}+\frac{{\left(4-1\right)}^{2}}{{b}^{2}}=1\to \frac{{3}^{2}}{{b}^{2}}=1\to b=3
Vamos con el segundo punto.
ec2:\frac{{\left(0-1\right)}^{2}}{{a}^{2}}+\frac{{\left(1-1\right)}^{2}}{{b}^{2}}=1\to \frac{{1}^{2}}{{a}^{2}}=1\to a=1
Sustituyendo en la ecuación:
\frac{{\left(x-1\right)}^{2}}{1}+\frac{{\left(y-1\right)}^{2}}{9}=1
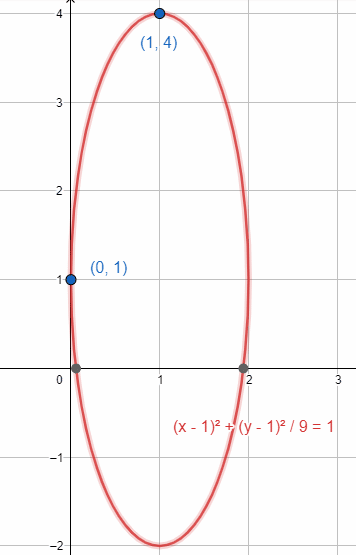
Concluimos que la respuesta correcta es el inciso b).
Lista de carreras por ciudad en UABC
Reactivo 34
A partir de la siguiente fracción algebraica, determine su descomposición en fracciones parciales.
\frac{1}{x\left(x-1\right)\left(x+1\right)}
- -\frac{1}{x}+\frac{1}{3\left(x-1\right)}-\frac{1}{2\left(x+1\right)}
- -\frac{1}{x}+\frac{1}{2\left(x-1\right)}+\frac{1}{2\left(x+1\right)}
- \frac{1}{2x}-\frac{1}{x-1}+\frac{1}{2\left(x+1\right)}
Solución:
Para descomponer a una fracción en otras más simples, igualamos a la fracción original a tantas fracciones como factores tenga en el denominador. Como esta tiene 3 factores, la igualamos a 3 fracciones simples.
\frac{1}{x\left(x-1\right)\left(x+1\right)}=\frac{A}{x}+\frac{B}{x-1}+\frac{C}{x+1}
Ahora, pasamos a multiplicar el denominador de la izquierda a la derecha.
1=A\left(x-1\right)\left(x+1\right)+Bx\left(x+1\right)+Cx\left(x-1\right)
Desarrollamos los productos.
1=A\left({x}^{2}-1\right)+B\left({x}^{2}+x\right)+C\left({x}^{2}-x\right)
Agrupamos términos semejantes.
1={x}^{2}\left(A+B+C\right)+x\left(B-C\right)-A
\left\{\begin{array}{c}A+B+C=0\\ B-C=0\\ -A=1\end{array}\right.
Iniciamos encontrando el valor de A .
A=-1
Desde la segunda ecuación obtenemos la siguiente igualdad.
B=C
Sustituimos en la primera ecuación.
-1+B+B=0\to 2B=1\to B=\frac{1}{2}
De tal forma que:
C=B=\frac{1}{2}
Sustituyendo en las fracciones parciales:
\frac{1}{x\left(x-1\right)\left(x+1\right)}=-\frac{1}{x}+\frac{1}{2\left(x-1\right)}+\frac{1}{2\left(x+1\right)}
Concluimos que la respuesta correcta es el inciso b).
Respuesta correcta: c).
Reactivo 35
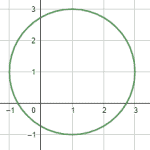
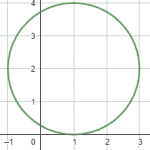
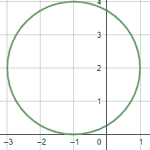
Indique la gráfica que corresponde con la circunferencia representada por la ecuación {x}^{2}-2x+{y}^{2}-2y+2=4 .
Solución:
Debido a que la circunferencia está dada en su forma general, debemos completar cuadrados tanto en x como en y para dar con la forma ordinaria.
Comenzamos descomponiendo los términos lineales como 2ax y 2by .
{x}^{2}-2x+{y}^{2}-2y+2=4\to {x}^{2}-2\left(1\right)x+{y}^{2}-2\left(1\right)y+2=4
En este caso a=b=1 , debemos ahora sumar en ambos miembros a y b .
{x}^{2}-2\left(1\right)x+1+{y}^{2}-2\left(1\right)y+1+2=4+1+1
Simplificando:
{x}^{2}-2\left(1\right)x+1+{y}^{2}-2\left(1\right)y+1=4
Ahora, aplicamos el producto notable del binomio al cuadrado en sentido contrario.
{x}^{2}-2\left(1\right)x+1+{y}^{2}-2\left(1\right)y+1=4\to {\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}=4
La forma ordinaria de la circunferencia es:
{\left(x-1\right)}^{2}+{\left(y-1\right)}^{2}={2}^{2}
El centro es \left(h,k\right)=\left(1, 1\right) y el radio r=2 .
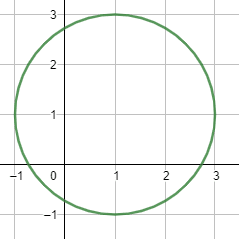
Examinando las figuras de los incisos, la única que cumple con esto es el inciso a).
Reactivo 36
En álgebra avanzada, se denominan simetrías a las transformaciones que se aplican sobre un objeto matemático que lo hacen permanecer invariante. Suponga que su objeto matemático es un cuadrado, ¿cuál es el mínimo ángulo de rotación no nulo, que mantiene al cuadrado invariante?
- 180°
- 45°
- 90°
Solución:
Aunque el enunciado inicia con una premisa intimidante, nuestra atención debe concentrarse en la última frase. Debemos encontrar un determinado ángulo de rotación (en sentido contrario a las agujas del reloj, por ejemplo) que mantenga al cuadrado igual que antes de rotar.
Si examinamos a un cuadrado cualquiera, nos daremos cuenta que el ángulo de rotación no nulo que mantiene invariante al cuadrado es 90°.
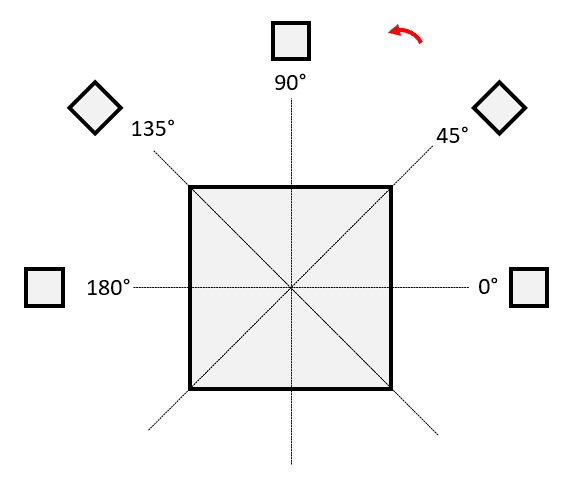
Concluimos que la respuesta correcta es el inciso c).
Reactivo 37
Es el resultado de la expresión:
3\left(8-4\right)+3\left(2-5\right)+{2}^{3}
- 26
- 11
- -3
Solución:
En este caso, debemos aplicar en el orden adecuado las reglas de la jerarquía de operaciones y signos de agrupación. Examinando la expresión, nos damos cuenta que 2 términos tienen paréntesis y que el tercero es una potencia. Según las reglas, primero resolvemos el interior de los paréntesis.
3\left(8-4\right)+3\left(2-5\right)+{2}^{3}=3\left(4\right)+3\left(-3\right)+{2}^{3}
Ahora, nos quedan 2 productos y la potencia. Se resuelve la potencia.
3\left(4\right)+3\left(-3\right)+{2}^{3}=3\left(4\right)+3\left(-3\right)+8
Vamos con los productos indicados con los paréntesis.
3\left(4\right)+3\left(-3\right)+8=12-9+8
Finalmente, las sumas y restas de izquierda a derecha.
12-9+8=3+8=11
La respuesta correcta es el inciso b).
Reactivo 38
Si se requieren 2 personas para construir una cerca de 15 m de largo y 2 m de alto en 2 días, ¿cuántas personas se necesitan para construir otro muro con el doble de área en 3 días?
- 3
- 5
- 4
Solución:
Para esta solución, debemos implementar una regla de tres compuesta. Nuestra variable x será la cantidad de obreros, mientras que el área de la cerca y el tiempo (días), serán los parámetros para establecer la relación.
Comencemos identificando la relación entre x y los parámetros.

Relación Tiempo – Obreros:
A mayor cantidad de obreros, menor será el tiempo del proyecto. Relación inversa.
Relación Superficie – Obreros:
A mayor cantidad de obreros, mayor área se puede construir a la vez. Relación directa.
Estableciendo la regla de tres compuesta nos queda:
\frac{x}{2}=\left(\frac{2}{3}\right)\left(\frac{60}{30}\right)\to x=2\left(\frac{2}{3}\right)\left(2\right)=2.66
Redondeando por exceso, se necesitan 3 obreros para construir una cerca de 60 metros cuadrados en 3 días. La respuesta correcta es el inciso a).
Reactivo 39
En un partido de béisbol, el bateador conecta un hit en línea recta hacia la tercera base. El jugador que cubre dicha posición captura la bola, pero necesita lanzar hacia la segunda base para concretar un doble play que terminaría el inning.
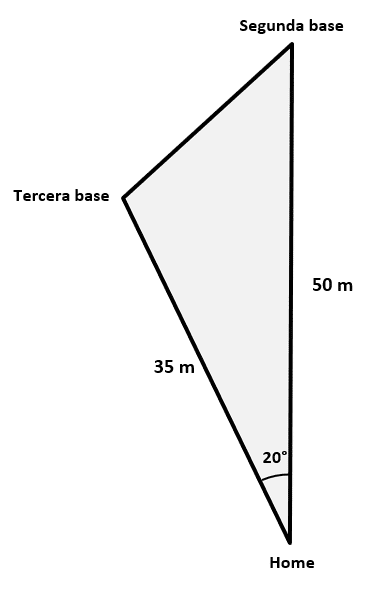
La figura anterior muestra la situación del lanzamiento. Calcula la distancia que debe recorrer la pelota.
- 55 \mathrm{m}
- 436 \mathrm{m}
- 20.88 \mathrm{m}
Solución:
Haciendo a un lado el contexto del enunciado, tenemos que calcular cuánto mide la arista desconocida del triángulo. Tengamos en cuenta que el triángulo es obtusángulo, por tanto, no podemos aplicar el teorema de Pitágoras.
En su defecto, nos queda aplicar la ley del coseno ya que conocemos 2 lados y 1 ángulo.
{c}^{2}={a}^{2}+{b}^{2}-2ab\mathrm{cos}\alpha
Donde c es el lado desconocido, a y b los conocidos y \alpha el ángulo opuesto a c . Sustituyendo nos queda:
{c}^{2}={35}^{2}+{50}^{2}-2\left(35\right)\left(50\right)\mathrm{cos}\left(20°\right)=436.08 {\mathrm{m}}^{2}
Aplicando raíz en ambos lados:
c=20.88 \mathrm{m}
La bola debe recorrer 20.88 metros.
La respuesta correcta es el inciso c).
Reactivo 40
María debe preparar 50 helados de chocolate para un pedido, donde cada vaso de helado tiene un volumen de 120 ml. Si utiliza medio litro de crema para batir, 150 ml de leche condensada y 100 ml de leche pasteurizada, ¿en qué proporción deberá incrementar María los ingredientes de la receta para cumplir con el pedido?
- 6
- 8
- 10
Solución:
Comencemos por calcular el volumen total de los 50 helados.
{\mathrm{V}}_{\mathrm{t}}=50\left(120 \mathrm{m}\mathrm{l}\right)=6000 \mathrm{m}\mathrm{l}
Ahora, sumemos los volúmenes de los ingredientes de la receta.
{\mathrm{V}}_{\mathrm{r}}=500 \mathrm{m}\mathrm{l}+150\mathrm{ }\mathrm{m}\mathrm{l}+100\mathrm{m}\mathrm{l}=750\mathrm{ }\mathrm{m}\mathrm{l}
En primera instancia, la receta de María no será suficiente para suplir el pedido. La proporción de los ingredientes se calcula como el cociente del volumen requerido sobre el volumen de la receta.
{P}_{v}=\frac{{\mathrm{V}}_{\mathrm{t}}}{{\mathrm{V}}_{\mathrm{r}}}=\frac{6000 \mathrm{m}\mathrm{l}}{750 \mathrm{m}\mathrm{l}}=8
María debe comprar 8 veces más crema para batir, leche condensada y leche pasteurizada para el pedido.
La respuesta correcta es el inciso b).