¿Vas a presentar el nuevo examen de UABC? En este simulacro vamos a resolver 50 ejercicios del área de pensamiento matemático del nuevo Exani II de Ceneval.

Recuerda que el examen de admisión que vas a presentar en UABC es el Exani II, y que es por especialidad, es decir que los temas varían dependiendo de la carrera a la que apliques.
¿Vendrá matemáticas en mi examen? Los temas cambian dependiendo del área de conocimiento de tu carrera, sin embargo existen tres áreas que vienen en todas las pruebas.
En resumen, matemáticas viene en el examen de admisión a todas las carreras a la UABC.
Antes de comenzar:
- Hemos dividido el simulacro en 5 partes, intenta resolver el examen en máximo 60 minutos.
- Antes de comenzar te recomiendo que leas la introducción al simulacro UABC 2023.
- El simulacro cubre todos los temas del examen de admisión en el área de pensamiento matemático.
- Si quieres ir directo a los primeros 10 reactivos, desplázate y comienza a resolver los ejercicios.
Lo más importante es que antes de consultar la solución, intentes resolver el simulacro por tu cuenta.
Estructura del examen de admisión
El nuevo examen a UABC se compone de 138 reactivos, de los cuales 30 corresponden a pensamiento matemático, y el resto a las materias que te presentamos en la siguiente tabla.
La primera parte del examen se conoce como examen de habilidades y conocimientos, y la segunda consiste en reactivos de temas relacionados con el area de conocimiento de tu licenciatura.
Estructura del examen UABC 2023
| Área | Reactivos |
|---|---|
| Examen de habilidades y conocimientos | 90 |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Examen de conocimientos específicos | 48 |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Total de reactivos | 138 |
| Diagnóstico de inglés | 30 |
| Total | 168 |
Si quieres conocer los módulos específicos, y la lista de carreras con los módulos correspondientes, en el artículo de la guía UABC 2023 podrás conocerlos, asi como el resto de los temas que tienes que estudiar.
Temario de pensamiento matemático
Los reactivos de matemáticas del examen de admisión UABC cubren diferentes ramas tales como: aritmética, estadística, geometría, trigonometría y álgebra.
No se trata de aprender fórmulas, debes entrenar tu capacidad de análisis para resolver problemas con matemáticas.
La siguiente lista contiene todos los temas que debes estudiar para responder esta parte del examen.
- Aritmética
- Jerarquía de operaciones básicas
- Relaciones de proporcionalidad
- Álgebra
- Expresiones algebraicas
- Productos notables
- Ecuaciones
- Sistemas de ecuaciones
- Ecuaciones con dos o tres incógnitas: solución gráfica y matemática
- Representaciones gráficas
- Probabilidad y estadística
- Frecuencias e información gráfica
- Uso e interpretación de tablas de frecuencias
- Gráficos para representar información (barras, circulares, de polígono)
- Medidas descriptivas
- Medidas de tendencia central (media, mediana y moda)
- Medidas de posición
- Nociones de probabilidad
- Geometría
- Puntos, segmentos y plano cartesiano
- Línea recta
- Trigonometría
- Funciones trigonométricas
- Función seno, coseno y tangente.
- Triángulos rectángulos u oblicuángulos
- Razones trigonométricas
¿Cómo resolver el examen simulacro?
Con las siguientes recomendaciones, podrás recrear las condiciones del examen real.
- Resuelve cada parte por tu cuenta sin mirar la solución
- Establece un tiempo no mayor a 20 minutos por cada 10 reactivos
- Analiza el procedimiento para resolver los ejercicios e intenta acortar el tiempo
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Debes mantener la concentración y no entrar en pánico
Reactivo 1
Un estudiante se encuentra a 15 m de una estructura para la que debe hacer un modelo a escala. El estudiante observa la parte alta de éste y se da cuenta que forma un ángulo de elevación de 55° respecto a su línea de visión (línea punteada).
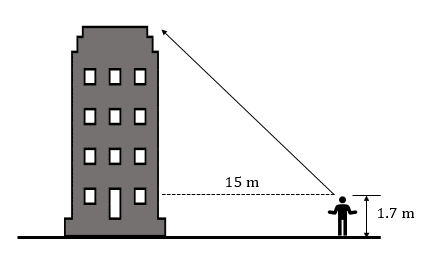
Considere que:
\begin{array}{c}\mathrm{sin}55°=0.82\\ \mathrm{cos}55°=0.574\\ \mathrm{tan}55°=1.428\end{array}¿Cuál debe ser la altura del edificio a escala, si el mismo debe ser 20 veces más pequeño que el original?
- 36.42 m
- 1.15 m
- 1.07 m
Solución:
Para resolver este problema, debemos emplear trigonometría; donde parte de la altura del edificio es el cateto opuesto al ángulo de elevación y el cateto adyacente es la distancia de 15 metros.
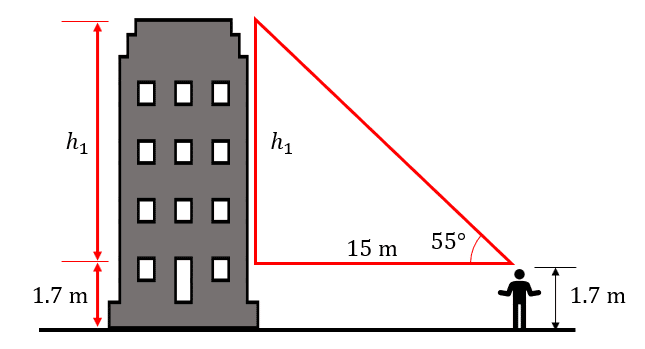
Empleamos la razón trigonométrica de la tangente para calcular {h}_{1} .
\mathrm{tan}55=\frac{{h}_{1}}{15}\to {h}_{1}=15tan55
{h}_{1}=21.42
Ahora, la altura total se obtiene sumando la altura del estudiante.
h=21.42+1.7=23.12
Finalmente, la altura de la maqueta se obtiene dividiendo por 20 la altura real del edificio.
{h}_{m}=\frac{h}{20}=\frac{23.12}{20}=1.15 \mathrm{m}
La maqueta debe medir 1.15 metros de altura.
La respuesta correcta es el inciso b).
Reactivo 2
Con base en la imagen, seleccione la operación que corresponda al área de la región sombreada. Tenga en cuenta que: BC=FG=1 , AB=CD=EF=GH=0.5 , AE=DH=1.5 .
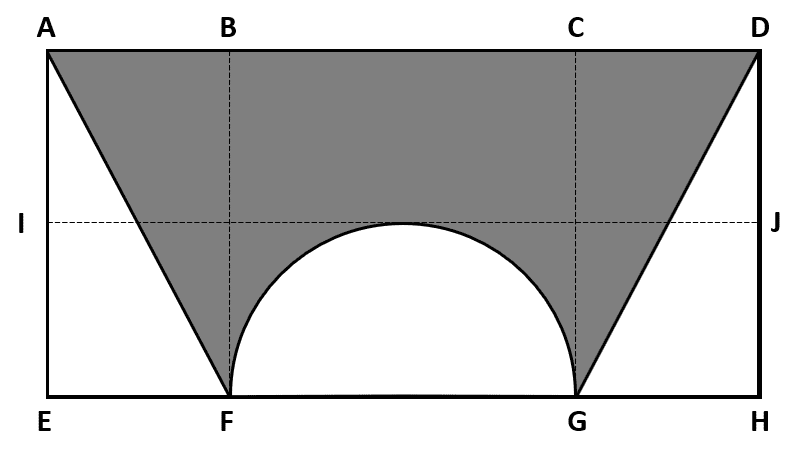
- 2-\frac{3}{8}\pi
- \frac{2}{3}-3\pi
- \frac{3}{2}-\frac{\pi }{8}
Solución:
Debemos comenzar identificando las figuras cuya suma o resta de áreas nos permitirán calcular a la región sombreada. Si al rectángulo exterior le restamos el área de las tres figuras blancas obtenemos la región sombreada:
{A}_{s}=AE\times EH-AEF-FGF-GDH
Ahora, calculamos el área de cada figura en blanco. Comenzamos con los triángulos que, además, son iguales.
AEF=GDH=\frac{GH\times DH}{2}=\frac{\left(1.5\right)\left(0.5\right)}{2}=0.75 {u}^{2}
Calculamos el área de la media circunferencia.
FGF=\frac{\pi {D}^{2}}{8}=\frac{\pi {FG}^{2}}{8}=\frac{\pi {1}^{2}}{8}=\frac{\pi }{8}
Finalmente, calculamos el área sombreada como:
{A}_{s}=\left(2\right)\left(1.5\right)-2\left(0.75\right)-\frac{\pi }{8}=\frac{3}{2}-\frac{\pi }{8}
El área sombreada tiene una superficie de \frac{3}{2}-\frac{\pi }{8} .
La respuesta correcta es el inciso c).
Reactivo 3
¿Qué opción es equivalente a la expresión 4{\left(x-y\right)}^{3}\left(2x-2y\right) ?
- 16{\left(x-y\right)}^{3}
- 8{\left(x-y\right)}^{4}
- 4{\left(x-y\right)}^{3}
Solución:
Comenzamos extrayendo el 2 factor común.
4{\left(x-y\right)}^{3}\left(2x-2y\right)=4\left(2\right){\left(x-y\right)}^{3}\left(x-y\right)=8{\left(x-y\right)}^{3}(x-y)
Finalmente, aplicamos la ley del producto de potencias de igual base.
8{\left(x-y\right)}^{3}\left(x-y\right)=8{\left(x-y\right)}^{4}
La respuesta correcta es el inciso b).
Reactivo 4
Se tienen tres espacios en un closet para ordenar 4 suéteres de colores diferentes: rojo, azul, morado y amarillo. Calcule la cantidad de formas en las que se pueden ordenar
- 6
- 4
- 2
Solución:
Para resolver cualquier problema de conteo, debemos iniciar respondiendo 3 preguntas:
- ¿Importa el orden?
- ¿Intervienen todos los elementos?
- ¿Hay elementos repetidos?
En este caso, debido a que no nos interesa qué suéter queda en primer lugar, ya que es irrelevante concluimos que no importa el orden, por tanto, se trata de una combinación donde no intervienen todos los elementos.
{C}_{m}^{n}=\frac{m!}{\left(m-n\right)!n!}
En nuestro caso m=4 y n=3 . Sustituimos.
{C}_{4}^{3}=\frac{4!}{\left(4-3\right)!3!}=\frac{4!}{1!3!}=\frac{4\times 3\times 2\times 1}{3\times 2\times 1}=4
Los suéteres se pueden ordenar de 4 formas distintas.
La respuesta correcta es el inciso c).
Reactivo 5
Un ingeniero recién graduado se encuentra en búsqueda de un empleo que le permita pagar su renta mensual de 650$, el mercado de 400$ y ahorrar unos 350$. Una empresa a las afueras de la ciudad le ha ofrecido una oportunidad, en la que ganará 55$ el día de trabajo. Además, puede trabajar 4 días extras a la semana con una remuneración de 350$ cada día.
Si la jornada laboral es de 5 días a la semana y el mes fiscal tiene 4 semanas, ¿cuántos días extra debe trabajar el ingeniero para cumplir con su mínimo mensual?
- x\le 1
- x>2
- x\ge 1
Solución:
El problema nos pide calcular la cantidad de días extra que debe trabajar el ingeniero recién graduado para cubrir el mínimo del mes. Comencemos por calcular cuánto es ese mínimo mensual que necesita.
\mathrm{m}\mathrm{e}\mathrm{s}=650\mathrm{\$}+400\mathrm{\$}+350\mathrm{\$}=1400\mathrm{\$}
Ahora, debemos establecer una ecuación entre los 1400$ y lo que gana al mes. Sabemos que trabaja 5 días a la semana, por 4 semanas al mes son 20 días de trabajo al mes. Por esos 20 días ganaría:
\mathrm{S}\mathrm{u}\mathrm{e}\mathrm{l}\mathrm{d}\mathrm{o}\mathrm{ }\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}=20\times 55\mathrm{\$}=1100\mathrm{\$}
Llamaremos x a los días extra que debe trabajar.
350x=1400-1100=300
Despejamos a la x :
x=\frac{300}{350}=0.857
Redondeando por encima, el ingeniero debe trabajar al menos un día extra al mes para cubrir sus gastos.
x\ge 1
Concluimos que la respuesta correcta es el inciso c).
Reactivo 6
Juliana tiene una tienda de repostería y planea ofrecer una promoción a sus clientes por el día de San Valentín. La oferta consiste en 1 pastel mediano y 12 pastelitos rellenos por 350$. Ella calcula que con su oferta aumentará en un 50% los pedidos de pasteles y pastelitos rellenos para el 14 de febrero. Si el pastel cuesta 250$ y los pastelitos rellenos 150$, ¿cuál es la diferencia en ganancias que obtiene Juliana?
- 125 pesos por venta
- 80 pesos por venta
- 130 pesos por venta
Solución:
Aunque el enunciado parezca extenuante y pueda resultar confuso, debemos calcular las ganancias que tendría Juliana con la promoción y a esto restarle lo que ganaría sin haber implementado la promoción.
El enunciado no indica el número de ventas, por lo que trataremos a dicha cantidad como x por ahora.
Ganancias con la promoción.
Las ventas incrementan un 50%, esto se traduce en 1.5x . Finalmente:
\mathrm{G}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{ó}\mathrm{n}=\mathrm{G}\mathrm{C}\mathrm{P}=1.5x\left(350\right)=525x
Ganancias sin la promoción.
Las ventas se mantienen iguales, es decir, x .
\mathrm{G}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{ }\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{ó}\mathrm{n}=\mathrm{G}\mathrm{S}\mathrm{P}=x\left(250+150\right)=400x
La diferencia entre las ganancias es:
\mathrm{D}=525x-400x=125x
Este resultado se puede interpretar como que hay una ganancia equivalente de 125$ por venta al implementar las promociones en lugar de las ventas normales.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 7
En un mercado, se dice que existe equilibrio entre la oferta y la demanda cuando…
- la cantidad de productos es muy grande
- la cantidad de productos y la demanda de ellos es igual
- la cantidad de compradores llega a un máximo histórico
Solución:
En términos financieros, un mercado es aquel establecido por la oferta de un producto (sea cual sea su naturaleza) y la disposición de compra por parte de los usuarios que participan en él. Ahora, lo que principalmente controla el precio de un activo en un mercado es la relación entre la oferta y la demanda.
Si hay mayor oferta que usuarios dispuestos a la compra, el precio del activo baja. Si hay mayor demanda (personas dispuestas a adquirirlo), el precio del activo subirá de cara al interés de las personas.
En síntesis y extendiendo la idea anterior, un mercado es estable cuando la oferta es igual a la demanda. Financieramente, se dice que el precio del activo está lateralizado. Podemos concluir, examinando los incisos, que la respuesta correcta es el b).
Reactivo 8
¿Cuál de las siguientes frases describe perfectamente el concepto de mediana?
- El elemento que divide en dos partes iguales al conjunto de datos
- El elemento con mayor incertidumbre respecto de la media
- El elemento que más se repite
Solución:
Según la estadística descriptiva, la mediana es el elemento que divide a una muestra en dos subconjuntos con la misma amplitud. Teniendo en cuenta esta sencilla definición y observando a los incisos, concluimos que la respuesta correcta es el a).
Reactivo 9
En la línea de producción de una empresa, se fabrican 400 piezas al día con la ayuda de 4 máquinas especializadas. Cada una de ellas genera piezas defectuosas, tal como se muestra en la siguiente tabla.
[table “865” not found /]Determine el porcentaje de piezas defectuosas que salen de la línea de producción por día.
- 0.875\%
- 87.5\%
- 8.75\%
Solución:
De entre las 400 piezas que se fabrican en la línea de producción en un día, las defectuosas corresponden a la suma de las piezas en mal estado que salen de cada máquina.
\mathrm{D}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{o}\mathrm{s}\mathrm{a}\mathrm{s}={\mathrm{M}}_{1}+{\mathrm{M}}_{2}+{\mathrm{M}}_{3}+{\mathrm{M}}_{4}
Sustituimos los valores de la tabla.
\mathrm{D}=10+5+12+8=35
El porcentaje de piezas defectuosas se calcula como el cociente entre defectuosas y el total de piezas por 100.
{\%}_{D}=\frac{35}{400}*100\%=8.75\%
El 8.75% de las piezas en la línea de producción salen defectuosas.
La respuesta correcta es el inciso c).
Reactivo 10
En la gráfica se muestra el número de bombillas led elaboradas por día hábil en una empresa de componentes eléctricos.
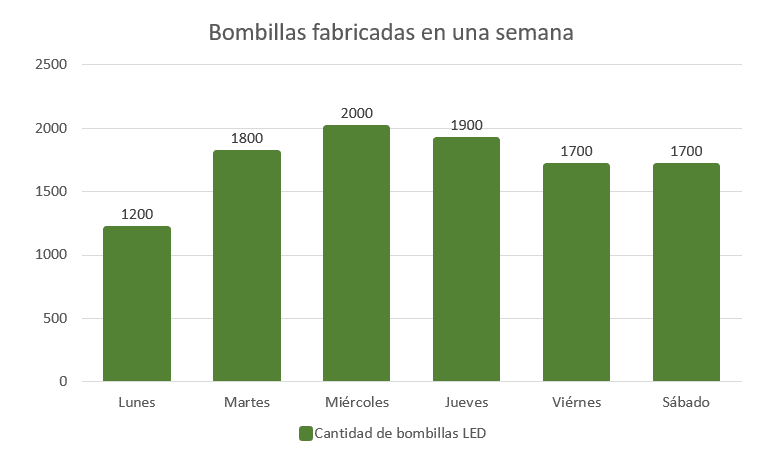
¿Cuál es la desviación típica de las bombillas fabricadas durante dicha semana?
- 254.4
- 354.4
- 2544
Solución:
A partir de la estadística descriptiva, sabemos que la desviación típica es un valor que mide el grado de dispersión dentro de un conjunto de datos. Mientras mayor sea la desviación típica \sigma , se dice que los datos se encuentran más dispersos respecto a la media.
Desviación típica para un conjunto universo de datos:
\sigma =\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}}
Donde {x}_{i} es el i-ésimo elemento, \stackrel{-}{x} es la media aritmética y N es el total de datos. Comencemos a calcular la media.
\stackrel{-}{x}=\frac{\sum {x}_{i}}{N}=\frac{1200+1800+2000+1900+1700+1700}{6}=1717
Ahora, calculamos el cuadrado de la diferencia entre cada elemento y la media.
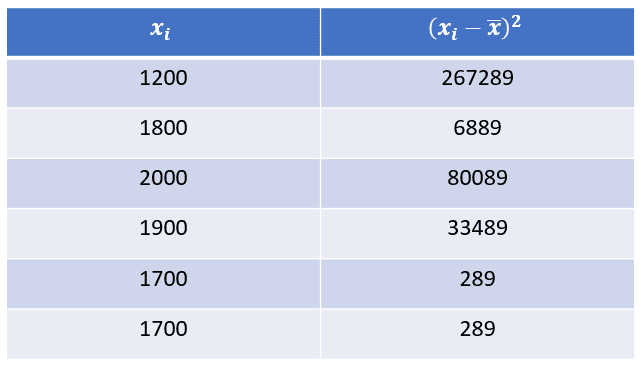
Sustituimos en la expresión de la desviación típica.
\sigma =\sqrt{\frac{267289+6889+80089+33489+289+289}{6}}=\sqrt{\frac{388334}{6}}=254.4
Concluimos indicando como respuesta correcta al inciso a).


