Hola de nuevo aspirante, continuamos con la segunda parte del simulacro de pensamiento matemático del nuevo examen de admisión a UABC. Vamos a resolver los reactivos del 11 al 20, recuerda utilizar un cronómetro en cada ejercicio.

Consulta los reactivos del 1 al 10 aquí
En el examen de admisión no basta con hacerlo bien, también debes hacerlo rápido, la mejor forma de desarrollar agilidad al momento de responder algún reactivo del examen es practicando.
Reactivo 11
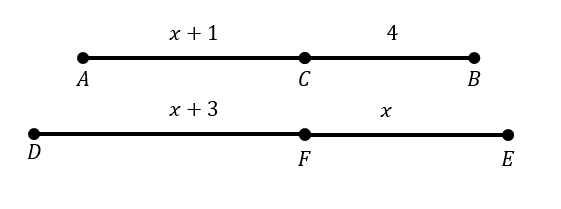
¿Dados los segmentos de la figura, para que valores de x se cumple la siguiente igualdad \frac{AC}{CB}=\frac{DF}{FE} ?
- 5.275
- \frac{22}{3}
- -2.275
Solución:
En este caso, las expresiones que se encuentran sobre los segmentos corresponden a sus longitudes.
AC=x+1, CB=4, DF=x+3, FB=x
Igualamos los cocientes de los segmentos.
\frac{x+1}{4}=\frac{x+3}{x}\to x\left(x+1\right)=4\left(x+3\right)
Resolviendo:
{x}^{2}+x=4x+12\to {x}^{2}-3x-12=0
Aplicamos la ecuación de segundo grado para calcular los posibles valores de x .
x=\frac{3\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-12\right)}}{2\left(1\right)}=\frac{3\pm \sqrt{9+48}}{2}=\frac{3\pm \sqrt{9+48}}{2}=\frac{3\pm \sqrt{57}}{2}
{x}_{1}=5.275, {x}_{2}=-2.275
Ahora, debemos sustituir los valores para comprobar que no haya resultados negativos. Saltamos la comprobación de {x}_{1} porque es positivo, vamos con {x}_{2} directamente.
AC=-2.275+1, CB=4, DF=-2.275+3, FB=-2.275
AC=-1.275, CB=4, DF=1.275, FB=-2.275
{x}_{2} no satisface las igualdades porque da como resultado segmentos negativos.
La respuesta correcta es el inciso a).
¿Ya conoces todos los temas del examen y su estructura?
Reactivo 12
La producción de un producto depende del nivel de demanda y de un cierto margen de stock que mantiene la empresa en caso de existir picos por parte de los consumidores. La siguiente tabla muestra las ventas de la empresa durante el primer semestre del año.
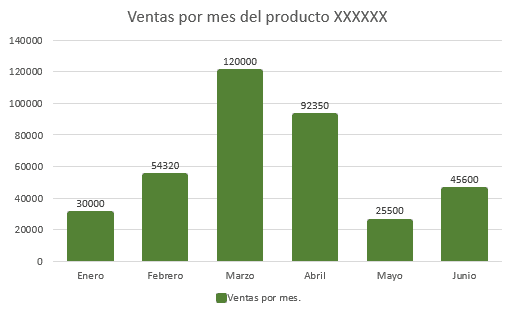
Actualmente, el departamento de producción se encuentra estimando el porcentaje de demanda para el segundo semestre del año. Si para el cálculo se toma en cuenta el mayor pico respecto a la media, ¿cuánto debería valer el margen de stock?
- 5.77\%
- 9.57\%
- 95.77\%
Solución:
Aunque el enunciado parezca extenuante, lo que debemos tener presente es que se nos pide calcular el porcentaje de stock. Ahora, dicho porcentaje se determina a partir de la media y del pico más alto en el semestre anterior. Comencemos calculando la media.
\stackrel{-}{x}=\frac{30000+54320+120000+92350+25500+45600}{6}=61295
Ahora, examinando la gráfica vemos que el pico más alto de ventas ocurrió en marzo con 120,000 ventas. A partir de dicho valor calculamos el porcentaje de stock.
{\%}_{s}=\frac{\mathrm{P}\mathrm{i}\mathrm{c}\mathrm{o}-\mathrm{M}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}}{\mathrm{M}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}}*100\%
Sustituimos:
{\%}_{s}=\frac{\mathrm{120,000}-\mathrm{61,295}}{\mathrm{61,295}}*100\%=95.77\%
El porcentaje de stock debe ser del 95.77%.
La respuesta correcta es el inciso c).
Reactivo 13
Identifique el camino más corto que permite ir desde el vértice A hasta el vértice F del grafo que se muestra en la figura.
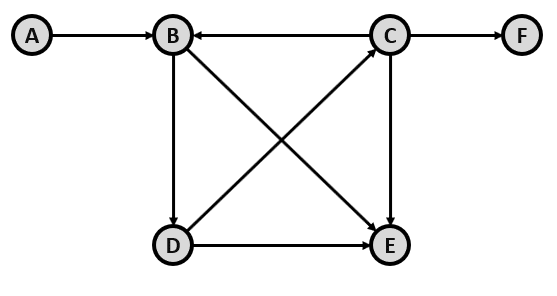
Tenga en cuenta que las flechas indican el sentido para avanzar de un vértice a otro.
- A B C F
- A B E C F
- A B D C F
Solución:
Para recorrer el grafo debemos tener algunas cosas presentes.
- Debemos iniciar desde el vértice A
- A menor cantidad de vértices recorridos, más rápido se llega a F
- La punta de las flechas indica el sentido de recorrido
Iniciando en A, la flecha nos indica que solo podemos desplazarnos hacia B.
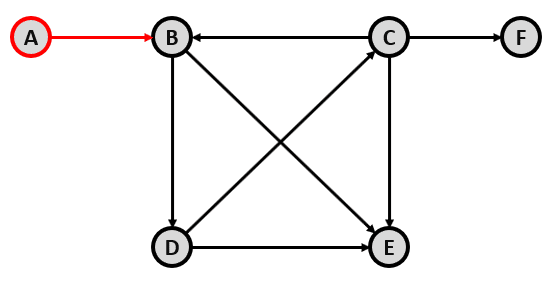
Ahora, tenemos dos opciones: ir hacia E o hacia D. Si vamos hacia E no podríamos salir de allí, al contrario de ir hacia la D. Vamos a desplazarnos hacia D.
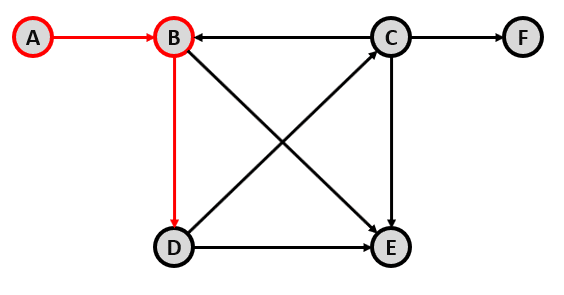
Siguiendo la misma lógica de antes, descartamos el camino hacia E y vamos directamente hacia C.
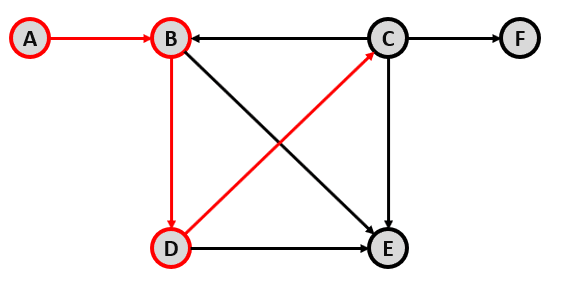
Finalmente, desde C vamos directo hacia F.
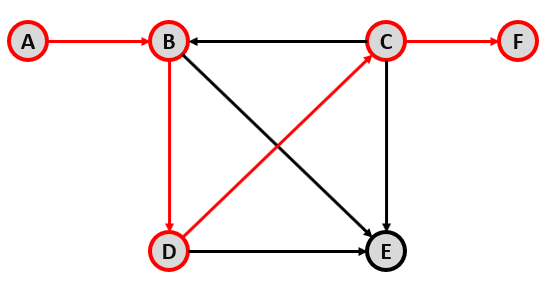
El recorrido es: A B D C F.
La respuesta correcta es el inciso c).
Conoce todo sobre el siguiente proceso de admisión a la UABC
Reactivo 14
En un juego de mesa inventado por dos hermanos, se lanza una moneda: si sale Cruz se tira una vez más, si sale Águila se tira un dado de 6 caras. Calcule la probabilidad de obtener a partir del dado, un número par en el juego.
- \frac{1}{6}
- \frac{1}{9}
- \frac{1}{4}
Solución:
Aunque el experimento aleatorio parezca complejo, nuestro mayor aliado en este caso será el diagrama de árbol.
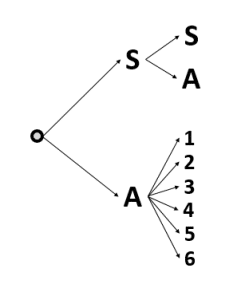
Para el primer lanzamiento, tenemos una probabilidad de \frac{1}{2} , mientras que la probabilidad de obtener luego un número par es de \frac{3}{6}=\frac{1}{2} .
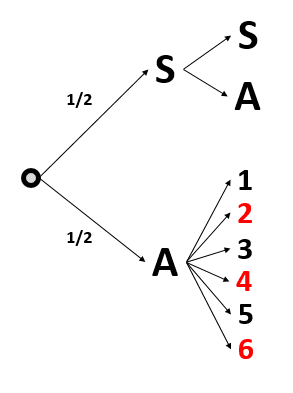
La probabilidad de obtener un número par en el juego es:
P\left(par\right)=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}=0.25
Los jugadores tienen una probabilidad de 0.25 para sacar un número par.
La respuesta correcta es el inciso c).
Lista completa de licenciaturas de la UABC
Reactivo 15
¿Qué tipo de simetría se muestra en la siguiente imagen?
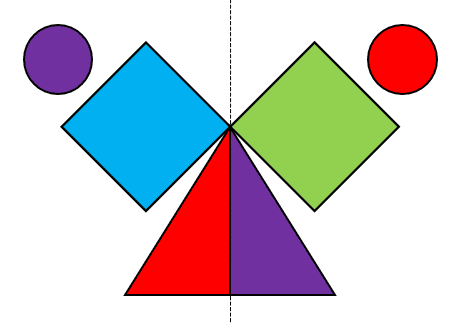
- Axial
- Central
- Esférica
Solución:
En geometría, las simetrías son aquellas relaciones que se pueden establecer entre dos o más figuras, teniendo en cuenta un eje o punto de simetría. Existen diferentes tipos de simetría, pero los más comunes son: las axial, central y la radial.
La simetría axial, es la que se da por reflexión de los objetos a partir de un eje de simetría. Esto es lo que ocurre en la figura del enunciado.
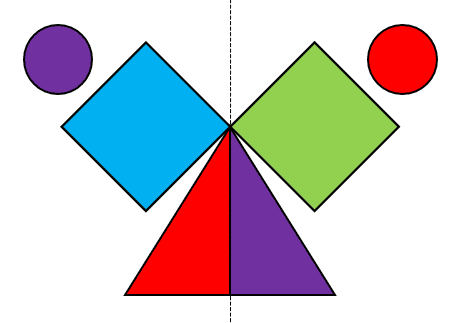
La simetría central ocurre respecto a un punto, donde los elementos homólogos se reflejan en una diagonal que pasa por el punto. Por otro lado, la simetría esférica ocurre a lo largo del radio de una circunferencia o de una esfera.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 16
Miguel y sus 3 amigos desean hacer una fiesta para celebrar que han sido seleccionados para ingresar en la universidad, gracias a determinado curso que tomaron. En la tienda toman 3 refrescos de 20$ cada uno, 2 paquetes de galletas por 10$ y 4 frituras a 12$ cada una.
Si al llegar a la caja el dependiente les dice que tienen el 20% de descuento, ¿cuánto dinero debe colocar cada uno?
- 20$
- 24$
- 30$
Solución:
Comencemos por sumar el total antes de aplicar el porcentaje de descuento.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{l}=3\mathrm{*}20+10+4\mathrm{*}12=118\mathrm{\$}
A esto, le debemos restar el 20% de descuento.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{u}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}=118\mathrm{*}0.8=94.4\mathrm{\$}
Finalmente, dividimos la cuenta entre los 4.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}=\frac{94.4\mathrm{\$}}{4}=23.6\$
Lo aproximamos a 24 pesos cada uno.
Comparando con los incisos, la respuesta correcta es el inciso b).
Reactivo 17
Complete la siguiente frase utilizando el concepto de regla de tres.
Un trabajador puede pintar un muro de 10 metros cuadrados en 4 horas, si ahora el muro es de 15 metros cuadrados y recibe ayuda de otro pintor, el trabajo se termina en _____ horas.
- 1 hora
- 2 horas
- 3 horas
Solución:
El enunciado nos dice que debemos recurrir al concepto de regla de tres, solo nos queda determinar dos cosas: inversa o directa y compuesta o no compuesta. En este caso tenemos en juego tres variables: la cantidad de pintores, el tiempo y la superficie del muro.
Ahora, el que sea directa o inversa depende de la relación entre las variables que estudiaremos a continuación.

Pintores – Tiempo: Al haber más pintores, el tiempo disminuye, por tanto, la relación es inversa.
Superficie – Tiempo: Si la pared tiene mayor superficie, tomará más tiempo pintarla, la relación es directa.
\frac{x}{4}=\left(\frac{1}{2}\right)\left(\frac{15}{10}\right)\to x=4\left(\frac{1}{2}\right)\left(\frac{15}{10}\right)=3 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
Para una pared de 15 metros cuadrados y dos pintores, el tiempo estimado es de 3 horas.
La respuesta correcta es el inciso c).
Reactivo 18
Calcule los valores de las constantes a y b que permiten factorizar la expresión \left(2{x}^{2}-3\right) de la siguiente forma: \left(ax-b\right)\left(ax+b\right) .
- a=\sqrt{2}, b=\sqrt{3}
- a=2, b=3
- a=\sqrt{3}, b=\sqrt{2}
Solución:
En este caso, debemos aplicar la factorización de la diferencia de cuadrados. Escribimos la raíz cuadrada de ambos términos en dos binomios conjugados.
Encontrando la raíz cuadrada de los términos.
\sqrt{2{x}^{2}}=\sqrt{2}x y \sqrt{3}
Ahora, escribimos estos resultados en el producto de binomios.
\left(\sqrt{2}x-\sqrt{3}\right)\left(\sqrt{2}x+\sqrt{3}\right)
De aquí extraemos que:
a=\sqrt{2} y b=\sqrt{3}
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 19
Desarrolle el siguiente binomio al cubo utilizando el producto notable correcto.
{\left(3y+\frac{1}{2}z\right)}^{3}
- 24{x}^{3}+36{x}^{2}y+18x{y}^{2}+3{y}^{3}
- {x}^{3}+36{x}^{2}y+18x{y}^{2}+3{y}^{3}
- 24{x}^{3}+36{x}^{2}+18x{y}^{2}+3{y}^{3}
Solución:
Para desarrollar la potencia al cubo del binomio, empleamos el siguiente producto notable.
{\left(a+b\right)}^{3}={a}^{3}+3{a}^{2}b+3a{b}^{2}+{b}^{3}
Llevándolo a nuestro binomio al cubo.
{\left(3y+\frac{1}{2}z\right)}^{3}={\left(3y\right)}^{3}+3{\left(3y\right)}^{2}\left(\frac{1}{2}z\right)+3\left(3y\right){\left(\frac{1}{2}z\right)}^{2}+{\left(\frac{1}{2}z\right)}^{3}
Simplificamos:
{\left(3y+\frac{1}{2}z\right)}^{3}=27{y}^{3}+\frac{27}{2}{y}^{2}z+\frac{9}{4}y{z}^{2}+\frac{{z}^{3}}{8}
Comparando con los incisos, indicamos como respuesta correcta al a).
Reactivo 20
Esteban desea comprar por internet algunos suministros para su negocio. En la tienda A puede adquirir el producto AAAA 100$ más económico, pero le llega dentro de 18 días, pero otro producto BBBB le sale 150$ más económico en la tienda B y le llega en 4 días.
¿Cuántas veces tiene que pedir Esteban el producto BBBB para que llegue el mismo día que el producto AAAA?
- 36 veces
- 2 veces
- 9 veces
Solución:
En este caso, debemos determinar cuántas veces se debe entregar el producto BBBB para que coincida con la fecha de entrega del producto AAAA. Primero, es necesario calcular el mínimo común múltiplo entre las cantidades.
MCM\left(18, 4\right)=36
Ahora, dividimos el 36 entre 4 para obtener la cantidad de veces que se entregó el producto BBBB.
\frac{36}{4}=9
El producto BBBB se debe entregar 9 veces a Esteban para que coincida con la entrega del producto AAAA. La respuesta correcta es el inciso c).

