Seguimos con la solución de la parte 3 del simulacro para el examen de admisión a la UABC de pensamiento matemático. Vamos a resolver los reactivos del 21 al 30, recuerda que durante el examen te vas a encontrar ejercicios de todas las áreas de matemáticas de la preparatoria.

Ejercicios del 11 al 20 del simulacro examen UABC
Recuerda que durante el curso abarcamos el 100% de los temas del examen de ingreso a la UABC, si quieres conocer todas las ventajas del curso ingresa al siguiente enlace.
Reactivo 21
¿Cuál es el área de la figura que se muestra en la figura?
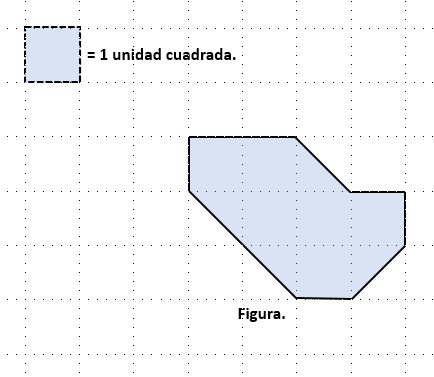
- 6 metros cuadrados
- 8 metros cuadrados
- 4 metros cuadrados
Solución:
Debido a que la cuadrícula sobre la que está dibujada la figura es cuadrada, vemos que las líneas diagonales cortan a los cuadrados, por tanto, sus áreas corresponden a la de medio cuadrado. Debemos contar los cuadrados completos por un lado y los medios cuadrados por otro, multiplicarlos por el área de cada uno y luego sumarlas. El resultado será el área de la figura.
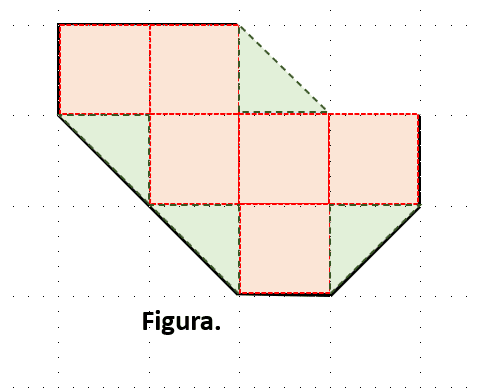
En la figura hay 6 cuadrados completos (indicados en rojo) y 4 medios cuadrados que juntos forman dos cuadrados enteros, por tanto, hay el equivalente a 8 cuadrados completos.
\mathrm{Á}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{ }\mathrm{f}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{r}\mathrm{a}=8\times 1{\mathrm{m}}^{2}=8 {\mathrm{m}}^{2}
La figura tiene un área de 8 metros cuadrados.
Concluimos que la respuesta correcta es el inciso b).
Todo sobre el siguiente proceso de ingreso a la UABC
Reactivo 22
Dados los polinomios {x}^{3}+2x-1 y x+1 , calcule su división.
- {x}^{2}+x+3+\frac{2}{x-1}
- {x}^{2}+x+3-\frac{1}{x-1}
- {x}^{2}+x+3-\frac{2}{x-1}
Solución:
Emplearemos el algoritmo de la división sintética.
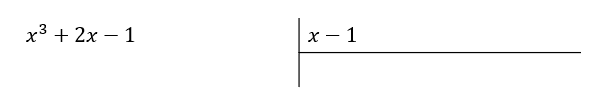
Comenzamos encontrando un monomio que multiplicado por x de como resultado -{x}^{3} . Recordemos que los resultados se escriben con el signo cambiado. Dicho monomio es {x}^{2} .
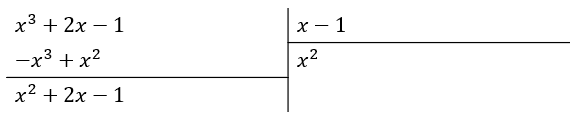
Ahora, sumamos el término x para que multiplicado con x-1 elimine a {x}^{2} .
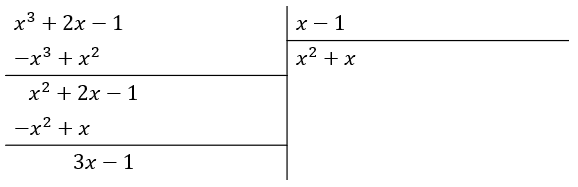
Finalmente, sumamos el término +3 para eliminar al 3x .
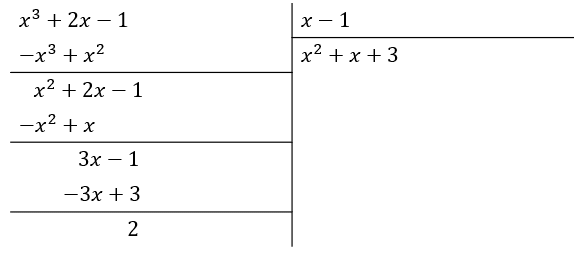
Este resultado quedaría expresado como:
\frac{{x}^{3}+2x-1}{x-1}={x}^{2}+x+3+\frac{2}{x-1}
La respuesta correcta es el inciso a).
Reactivo 23
En un experimento aleatorio, se tiene una caja con 6 bolas rojas y 4 bolas azules. Si no puedes devolver ninguna bola, ¿cuál es la probabilidad de obtener una bola roja al sacar una segunda vez?
- \frac{10}{15}
- \frac{12}{15}
- \frac{11}{15}
Solución:
En este caso, emplearemos el diagrama de árbol del experimento al sacar dos veces, para observar cómo cambia la probabilidad.
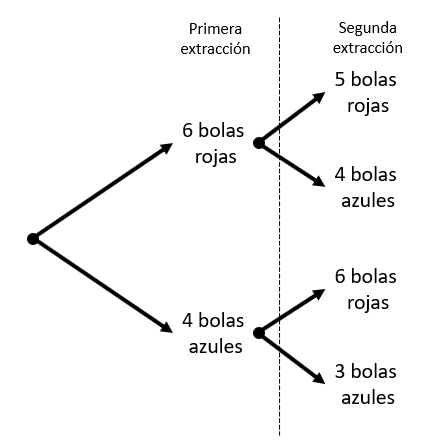
En el diagrama de árbol podemos darnos cuenta que el experimento se divide en dos ramas: una donde primero se saca una bola azul y otra donde sale una bola roja. A partir de ambos casos, al meter la mano en la caja una segunda vez, las probabilidades son distintas.
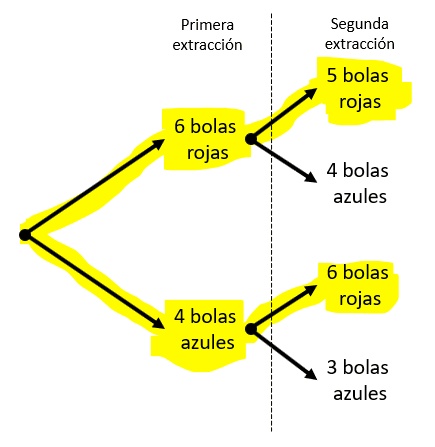
La probabilidad total será la suma de las probabilidades en ambos eventos, ya que son mutuamente excluyentes.
Probabilidad de extraer una bola roja, al haber sacado una roja en la primera.
{P}_{a}=\frac{6}{10}*\frac{5}{9}=\frac{1}{3}
Probabilidad de extraer una bola rota, al haber sacado una azul en la primera.
{P}_{b}=\frac{6}{10}*\frac{6}{9}=\frac{2}{5}
Probabilidad total:
P={P}_{a}+{P}_{b}=\frac{1}{3}+\frac{2}{5}=\frac{11}{15}\approx 0.733
La probabilidad de sacar una bola roja en la segunda extracción es de 0.733.
La respuesta correcta es el inciso c).
Reactivo 24
¿Cuál es la solución de la siguiente inecuación?
2x-\frac{1}{2}>x+3
- x\in \left(\frac{7}{2}, \infty \right)
- x\in \left(\infty , \frac{1}{2}\right)
- x\in \left(-\infty , \frac{7}{2}\right]
Solución:
Para resolver cualquier inecuación, debemos seguir las reglas de las desigualdades, especialmente tener cuidado al multiplicar o dividir por un número negativo, ya que esto haría cambiar el sentido de la desigualdad. Comencemos por agrupar las x hacia el miembro de la izquierda.
2x-x>\frac{1}{2}+3
Resolvemos.
x>\frac{7}{2}
La desigualdad se cumple para todo x mayor que \frac{7}{2} .
x\in \left(\frac{7}{2}, \infty \right)
Concluimos indicando como respuesta correcta al inciso a).
Consulta el temario completo del examen y las áreas con la nueva guía de estudios
Reactivo 25
A partir de las curvas que se muestran a continuación, ¿cuáles son sus puntos de intercepción?
{x}^{2}+{y}^{2}=1
y=x
- \left(\pm \sqrt{\frac{1}{2}},\mp \sqrt{\frac{1}{2}}\right)
- \left(\pm \sqrt{\frac{1}{2}},\pm \sqrt{\frac{1}{2}}\right)
- \left(\sqrt{\frac{1}{2}},-\sqrt{\frac{1}{2}}\right)
Solución:
Para encontrar los puntos de intersección, debemos resolver el sistema de ecuaciones no lineales.
\left\{\begin{array}{c}{x}^{2}+{y}^{2}=1\\ y=x\end{array}\right.
Comencemos por sustituir y por x en la ecuación de la circunferencia.
{x}^{2}+{x}^{2}=1\to 2{x}^{2}=1
\therefore x=\pm \sqrt{\frac{1}{2}}
Tenemos dos valores de x :
{x}_{1}=\sqrt{\frac{1}{2}} , {x}_{2}=-\sqrt{\frac{1}{2}}
Los valores de y se obtienen sustituyendo a x en la ecuación de la recta, por su evidente conveniencia.
y=\pm \sqrt{\frac{1}{2}}
{y}_{1}=\sqrt{\frac{1}{2}} , {y}_{2}=-\sqrt{\frac{1}{2}}
Gráficamente, la intercepción quedaría como:
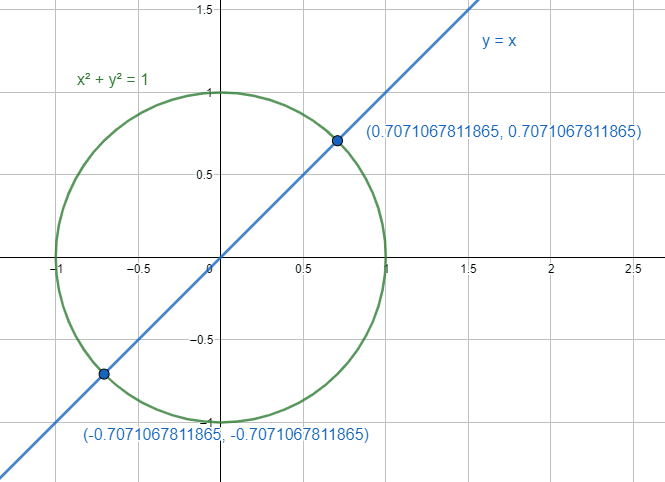
La respuesta correcta es la opción b).
Reactivo 26
Se tiene un experimento aleatorio en el que se lanzan 2 dados de 6 caras. Calcule la probabilidad de que la suma de las caras sea menor que 5.
- 6
- \frac{1}{36}
- \frac{1}{6}
Solución:
A partir de los dos dados, se pueden obtener 36 resultados diferentes.
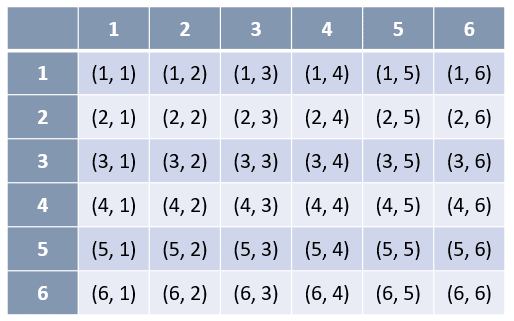
Ahora, a partir de esta tabla identificamos los pares que suman menos de 5.
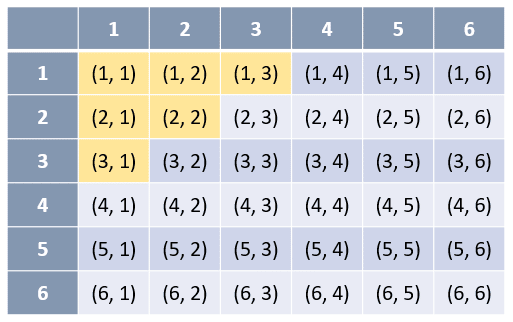
En la tabla contamos 6 pares de resultados que suman menos de 5. Aplicando la fórmula de probabilidad de Laplace:
P\left(+<5\right)=\frac{6}{36}=\frac{1}{6}
La probabilidad de que las caras sumen menos de 5 es de \frac{1}{6}=0.166 .
La respuesta correcta es el inciso c).
Conoce las carreras ofertadas por ciudad en UABC
Reactivo 27
A partir del siguiente conjunto de ecuaciones, ¿cuál de las tres aseveraciones es correcta?
\left\{\begin{array}{c}3x-y+z=1\\ x+y-z=0\end{array}\right.
- El sistema es compatible determinado
- El sistema es incompatible
- El sistema puede ser compatible indeterminado o incompatible
Solución:
El sistema del enunciado posee 2 ecuaciones y 3 incógnitas, por tanto, descartamos la posibilidad de que sea compatible determinado, porque no podremos encontrar una única solución. Esto nos deja con dos soluciones posibles: compatible indeterminado (infinitas soluciones) o incompatible (ninguna solución).
Aunque en este punto ya podríamos responder el enunciado, vale la pena justificar las posibilidades antes indicadas. Partamos del hecho de que ambas ecuaciones describen a planos en el espacio tridimensional y su intercepción pasa por la solución del sistema de ecuaciones.
Si continuamos con el enfoque geométrico, dichos planos podrían ser: equivalentes (el mismo plano), secantes (la intercepción sería una recta) o ser paralelos (no tener ningún punto en común). En las dos primeras tenemos infinitas soluciones y en la segunda ninguna.
Finalmente, diremos que existen formas sencillas de comprobar estas tres alternativas: comparando los vectores normales de los planos. Debido a que esto sobrepasa las intenciones del ejercicio, lo dejamos al aspirante como tarea.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 28
¿Cuál es el valor de \mathrm{tg}x , si se tiene que \mathrm{c}\mathrm{o}\mathrm{s}x=\frac{1}{2} ?
- \frac{2}{\sqrt{3}}
- \frac{2}{1}
- \frac{\sqrt{3}}{2}
Solución:
Este problema puede ser resuelto de dos formas sin recurrir a una calculadora científica: a través de transformaciones trigonométricas o mediante trigonometría. En cualquier caso, la mejor alternativa es emplear trigonometría.
A partir del coseno obtenemos: \mathrm{cos}x=\frac{1}{2}=\frac{CA}{H} .
CA=1, H=2
Dibujando el triángulo nos queda:
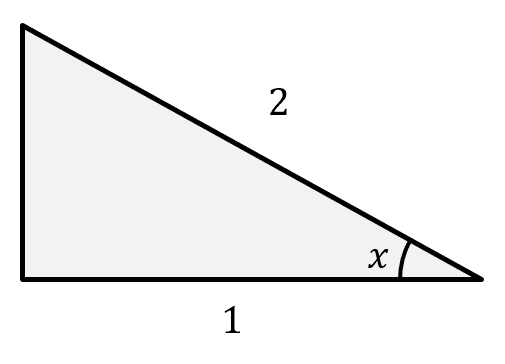
Para calcular la tangente, necesitamos al cateto opuesto y al adyacente. Al opuesto lo calculamos con Pitágoras.
CO=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}
Sustituyendo en la tangente de x .
\mathrm{tan}x=\frac{CO}{CA}=\frac{\sqrt{3}}{2}
La tangente de x es igual a \frac{\sqrt{3}}{2} .
Concluimos que la respuesta correcta es el inciso c).
Reactivo 29
¿Cuál de las siguientes expresiones corresponde a los valores que anulan a la función tangente?
- n\pi
- 2n\pi
- \frac{\pi \left(1+2n\right)}{2}
Solución:
Comencemos recordando que la tangente es una función trigonométrica representada por el cociente entre el seno y el coseno.
\mathrm{tan}x=\frac{\mathrm{sin}x}{\mathrm{cos}x}
Dicho cociente se anula cuando el seno se anula. En otras palabras, la tangente se anula en los mismos valores que el seno. Recordando la gráfica del seno, esta se anula en 0, \pi , 2\pi , 3\pi , \dots es decir en n\pi , donde n\ge 0 .
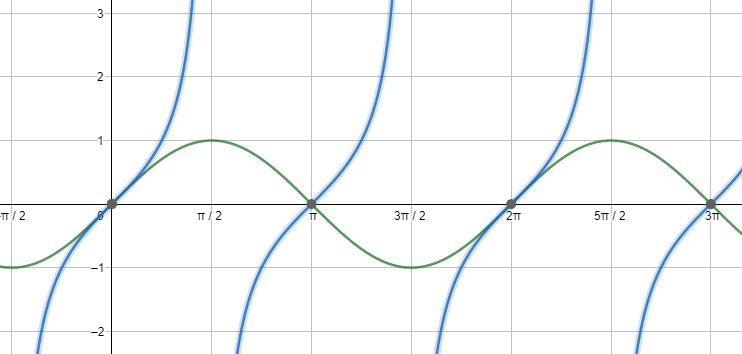
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 30
¿A qué valor tiende el seno cuando el ángulo \alpha tiende a infinito?
- -1
- 1
- Indefinido
Solución:
El seno es un tipo de función cíclica cuyo rango se encuentra acotado entre 1 y -1 incluidos los extremos, a lo largo del eje x . Teniendo esto en cuenta, a medida que hacemos crecer a x , las imágenes del seno continuarán oscilando entre 1 y -1 hasta el infinito.
Lo anterior establece que es imposible asignar un valor al seno cuando el ángulo tiende a infinito. Visto desde una perspectiva geométrica sobre la circunferencia trigonométrica, hacer que el ángulo crezca infinitamente significa girar en sentido contrario a las manecillas del reloj sin parar sobre el contorno de una circunferencia de radio unitario.
Concluimos entonces que la respuesta correcta es el inciso c).

